相關產品推薦更多 >>
如何消除自來水流量計信號中的工頻干擾問題
點擊次數:1882 發布時間:2020-08-03 06:24:19
隨著微電子技術的發展 ,自來水流量計的技術性能有了進一步的提高 ,應用也越來越廣泛 。由于其具有對液體適應性較強的特點 ,在現代工業生產中 ,成為測量流體流量的*選儀表。在現行的自來水流量計中 ,低頻矩形波勵磁方式已成為主要的勵磁方式 ,為了解決工頻干擾問題 ,實現對流體流速感應電勢 e ab 信號的準確測量 ,需利用以下基本關系:
①勵磁周期為工頻周期的整數倍,即勵磁頻率為50 n Hz(n 為偶數);
②正負勵磁下的同相位采樣。圖1 是對應低頻矩形波勵磁形式下的典型電勢信號形式,按上述關系在一個勵磁周期下 ,若假設 t 1 和 t 2 點為工頻干擾的等效干擾點 , 且采樣寬度 T =T 1 =T 2 ,則 e ab 的基本算式為
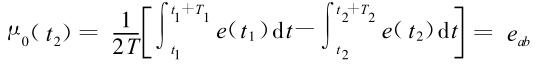
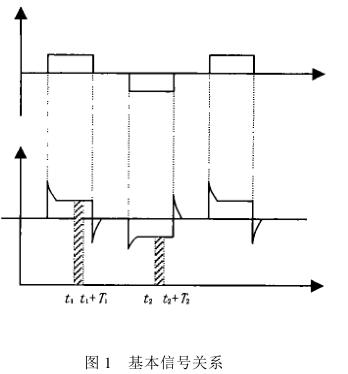
上式說明自來水流量計的工頻干擾在理論上有了可克服的途徑 ,但其方法是以同相位(t 1 =t 2 ), 同寬度采樣(T 1 =T 2 =T)為前提的 。顯然在實際情況下, 是不可能完全滿足這兩個前提的 ,采樣的相位與寬度不可避免地存在著誤差, 如何減少采樣誤差正是本文所要討論的問題。
1 工頻干擾對流量信號的影響
當流體流速較大時, 工頻干擾可以忽略, 并不是沒有,而是影響不敏感 ,這是相對感應電勢的值與工頻干擾的大小比較而言的 ;而當激勵電流減小(減小勵磁電功率)或流體流速較小時 ,發現工頻干擾值在與反映流速的信號值在同一個數量級上, 這時工頻干擾又顯得十分敏感。
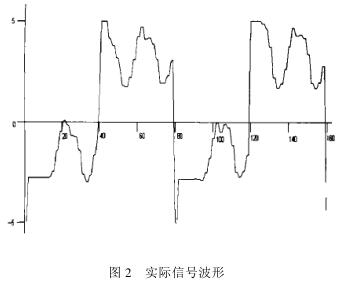
圖2 即為小流量 、激勵電流 <70 mA 時, 利用反饋式信號放大處理方法放大了 104數量級倍的信號波形。從圖中可以看出工頻干擾在實際信號中占的比例相當大 ,如果不正確地消除工頻干擾 ,就無法得到令人滿意的測量結果。
2 信號采樣方法的分析
長期以來, 在對自來水流量計進行信號處理時, 人們往往忽略了對信號采樣方法的分析 。實際上 ,采樣的區域、寬度、對稱度及采樣的起始點的選取 , 特別是在小流量情況下, 對自來水流量計的測量精度有較大的影響。為了說明問題, 下面對勵磁頻率為工頻的兩分頻和四分頻的情況進行分析 。
2.1 采樣頻率為工頻的兩分頻
采樣頻率為工頻的兩分頻如圖 3 所示 。

設為信號采樣起始相位角 ;T 為采樣寬度;ξ為采樣寬度誤差 ,令(為采樣相位誤差), 則其采樣信號誤差為
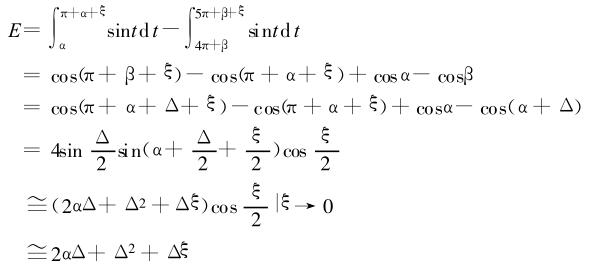
2.2 采樣頻率為工頻的四分頻
圖4(a)~ (c)直觀地描述了不同采樣寬度及采樣起始點位置對流量信號的影響 。設為信號采樣起始相位角,令為相位差 ;為采樣寬度誤差 都很小 ,可視為無窮小 。圖4(a)的采樣寬度為誤差為
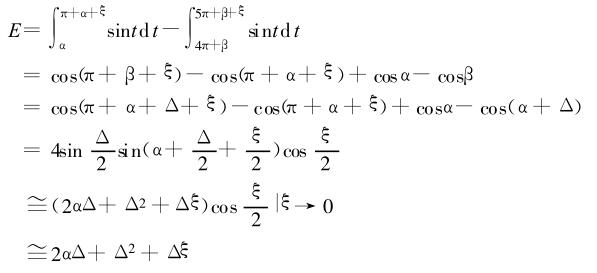
圖4(b)的采樣寬度也為但是采樣起始點向左平移了2,誤差為
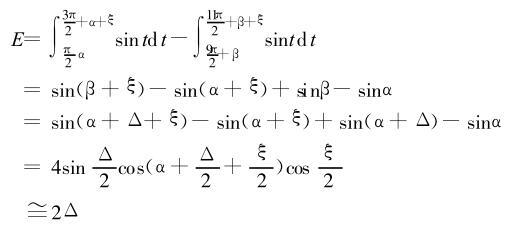
圖4(c)的采樣寬度為 2誤差為
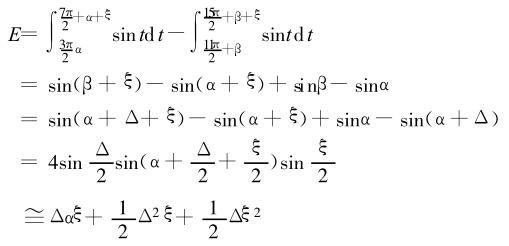
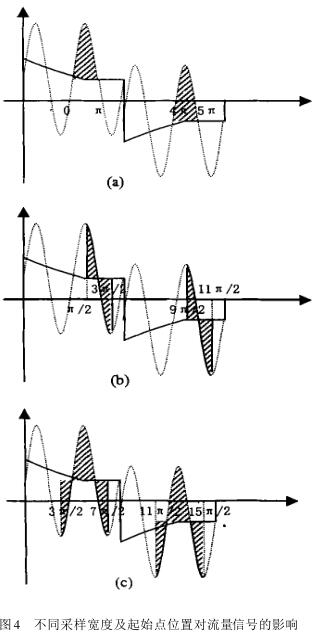
從以上算式可以看出 ,3 種采樣范圍都存在著誤差,就采樣誤差而言, 圖 4(a)近似于二階無窮小, 圖 4(b)似于一階無窮小 , 圖 4(c)近似于三階無窮小。因此采樣起始點及寬度如圖 4(c)時誤差 E *小 。對于六分頻、八分頻等情況,同樣有上述的結論。
3 實際信號波形的分析
就圖 2的實際信號波形(采樣頻率為工頻的四分頻)而言, 信噪比大約達到了 50%, 當假設正勵磁時間段的采樣起始點比負勵磁時間段滯后 1 ms, 即相位差Δ為 0.1π, 按上述 3 種采樣范圍 , 得到的采樣誤差分別為 0.049、0.309、0.000;如果假設正勵磁時間段的采樣寬度比負勵磁時間段大 0.1π, 即 ξ為0.1π,同樣按 3種情況進行采樣 , 得到的采樣誤差分別為 0.024、0.155、0.155 ;如果同時考慮上述兩種情況(假設條件不變),得到的采樣誤差分別為 0.120、0.448、0.139。由此可以看出,在采樣寬度及采樣起始點位置存在誤差時,圖 4(c)所示的采樣方法無論在哪一種情況下都能更好地克服工頻干擾 ,同理論分析的結果相一致。
4 結束語
由上面的分析不難發現 ,在對自來水流量計進行信號處理時 ,采樣寬度與采樣起始點對測量精度有著較大的影響 ,對采樣范圍的正確選取 ,將有利于電磁流量
計的測量精度的提高 。
利用上述采樣方法進行信號處理時 , 可以更好地消除工頻干擾, 使測量時具有高精度和超寬量程, 現在的 自來水流量計即為實現了*大動態量程范圍為0.001~ 10 m s 的正負雙向流量測量、精度達 0.5%RS(流速在 0.1~ 10 m s), 誤差 <0.000 5 m s(流速 <0.1 m s)的高性能自來水流量計。
①勵磁周期為工頻周期的整數倍,即勵磁頻率為50 n Hz(n 為偶數);
②正負勵磁下的同相位采樣。圖1 是對應低頻矩形波勵磁形式下的典型電勢信號形式,按上述關系在一個勵磁周期下 ,若假設 t 1 和 t 2 點為工頻干擾的等效干擾點 , 且采樣寬度 T =T 1 =T 2 ,則 e ab 的基本算式為
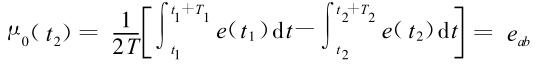

上式說明自來水流量計的工頻干擾在理論上有了可克服的途徑 ,但其方法是以同相位(t 1 =t 2 ), 同寬度采樣(T 1 =T 2 =T)為前提的 。顯然在實際情況下, 是不可能完全滿足這兩個前提的 ,采樣的相位與寬度不可避免地存在著誤差, 如何減少采樣誤差正是本文所要討論的問題。
1 工頻干擾對流量信號的影響
當流體流速較大時, 工頻干擾可以忽略, 并不是沒有,而是影響不敏感 ,這是相對感應電勢的值與工頻干擾的大小比較而言的 ;而當激勵電流減小(減小勵磁電功率)或流體流速較小時 ,發現工頻干擾值在與反映流速的信號值在同一個數量級上, 這時工頻干擾又顯得十分敏感。
圖2 即為小流量 、激勵電流 <70 mA 時, 利用反饋式信號放大處理方法放大了 104數量級倍的信號波形。從圖中可以看出工頻干擾在實際信號中占的比例相當大 ,如果不正確地消除工頻干擾 ,就無法得到令人滿意的測量結果。

2 信號采樣方法的分析
長期以來, 在對自來水流量計進行信號處理時, 人們往往忽略了對信號采樣方法的分析 。實際上 ,采樣的區域、寬度、對稱度及采樣的起始點的選取 , 特別是在小流量情況下, 對自來水流量計的測量精度有較大的影響。為了說明問題, 下面對勵磁頻率為工頻的兩分頻和四分頻的情況進行分析 。
2.1 采樣頻率為工頻的兩分頻
采樣頻率為工頻的兩分頻如圖 3 所示 。

設為信號采樣起始相位角 ;T 為采樣寬度;ξ為采樣寬度誤差 ,令(為采樣相位誤差), 則其采樣信號誤差為
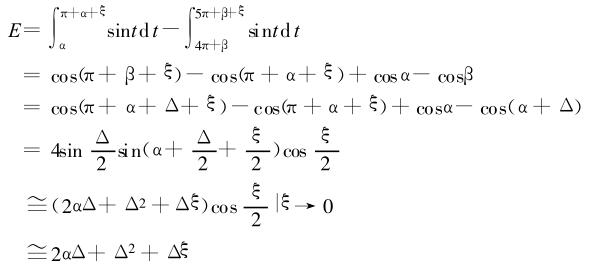
2.2 采樣頻率為工頻的四分頻
圖4(a)~ (c)直觀地描述了不同采樣寬度及采樣起始點位置對流量信號的影響 。設為信號采樣起始相位角,令為相位差 ;為采樣寬度誤差 都很小 ,可視為無窮小 。圖4(a)的采樣寬度為誤差為
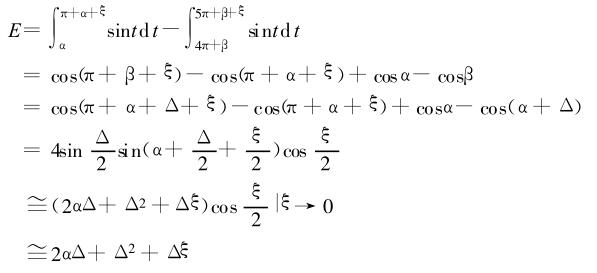
圖4(b)的采樣寬度也為但是采樣起始點向左平移了2,誤差為
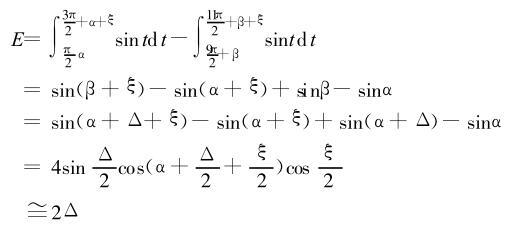
圖4(c)的采樣寬度為 2誤差為
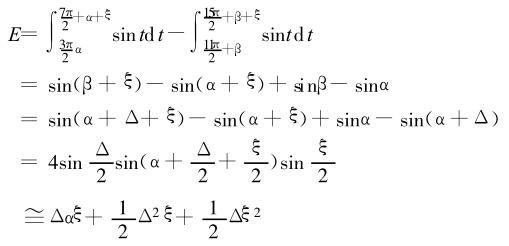

從以上算式可以看出 ,3 種采樣范圍都存在著誤差,就采樣誤差而言, 圖 4(a)近似于二階無窮小, 圖 4(b)似于一階無窮小 , 圖 4(c)近似于三階無窮小。因此采樣起始點及寬度如圖 4(c)時誤差 E *小 。對于六分頻、八分頻等情況,同樣有上述的結論。
3 實際信號波形的分析
就圖 2的實際信號波形(采樣頻率為工頻的四分頻)而言, 信噪比大約達到了 50%, 當假設正勵磁時間段的采樣起始點比負勵磁時間段滯后 1 ms, 即相位差Δ為 0.1π, 按上述 3 種采樣范圍 , 得到的采樣誤差分別為 0.049、0.309、0.000;如果假設正勵磁時間段的采樣寬度比負勵磁時間段大 0.1π, 即 ξ為0.1π,同樣按 3種情況進行采樣 , 得到的采樣誤差分別為 0.024、0.155、0.155 ;如果同時考慮上述兩種情況(假設條件不變),得到的采樣誤差分別為 0.120、0.448、0.139。由此可以看出,在采樣寬度及采樣起始點位置存在誤差時,圖 4(c)所示的采樣方法無論在哪一種情況下都能更好地克服工頻干擾 ,同理論分析的結果相一致。
4 結束語
由上面的分析不難發現 ,在對自來水流量計進行信號處理時 ,采樣寬度與采樣起始點對測量精度有著較大的影響 ,對采樣范圍的正確選取 ,將有利于電磁流量
計的測量精度的提高 。
利用上述采樣方法進行信號處理時 , 可以更好地消除工頻干擾, 使測量時具有高精度和超寬量程, 現在的 自來水流量計即為實現了*大動態量程范圍為0.001~ 10 m s 的正負雙向流量測量、精度達 0.5%RS(流速在 0.1~ 10 m s), 誤差 <0.000 5 m s(流速 <0.1 m s)的高性能自來水流量計。


